2523. Fibonacci strings
Fibonacci sequence of strings is defined as
follows:
·
s1 = “b”,
·
s2 = “a”,
·
sk = sk-1 + sk-2 äëÿ k > 2
For example, s3 = “ab”, s4 =
“aba”, s5 =
“abaab” and so on.
Given positive integers n, m, l.
Print the substring sn which starts at position m and have
the length l.
Input. One line contains three positive
integers n, m and
l (1 ≤ n ≤ 40; 1 ≤ m ≤
length(Sn); 1 ≤ l ≤ 1000).
Output. Print the substring of sn which starts at position m and have the length l (the
length of the printed substring may be less if the length of the remainder of
the string sn, starting from position m, is
less than l).
|
Sample
input |
Sample
output |
|
5 3 10 |
aab |
SOLUTION
recursion, strings
Algorithm analysis
Let fib(i)
be the i-th Fibonacci number. Using the fact that sn = sn-1 + sn-2, we’ll look for a
substring located at positions [m … m + l] either in sn-1, or in sn-2, or at their
intersection – that is, the final substring is a concatenation of
the suffix sn-1 and the prefix sn-2.
Lets implement the
function solve(n, Left, Right), which returns the Fibonacci substring sn, lying in
positions from Left to Right inclusive.
If n = 1 or n = 2, return the
corresponding string consisting of one character (s1 =
b, s2 = a).
Since sn is a concatenation of the
strings sn-1 and
sn-2, let’s determine
which of these parts (sn-1
or sn-2) contains the required
substring. At the same time, we know the lengths sn-1 and sn-2
(this is why we compute the Fibonacci numbers in the fib array).
·
If Right ≤ fib(n – 1), then the resulting substring lies
entirely in sn-1.
Return solve(n – 1, Left, Right).
·
If Left > fib(n – 1), then the resulting substring lies
entirely in sn-2.
In this case, you should recompute the indices of the desired substring, namely, subtract
the length sn-1
from Left and Right. Return solve(n – 2, Left – fib(n – 1), Right – fib(n – 1)).
·
Otherwise, the resulting substring starts at sn-1 and ends at sn-2. You must return the
substring from sn-1
at positions [Left … fib(n – 1)] and concatenate with the
substring from sn-2
at positions [1 … Right – fib(n – 1)]. That is, return solve(n – 1, Left,
fib(n – 1)) + solve(n – 2, 1, Right – fib(n – 1)).
Example
Let n = 7, m = 6,
l = 7.
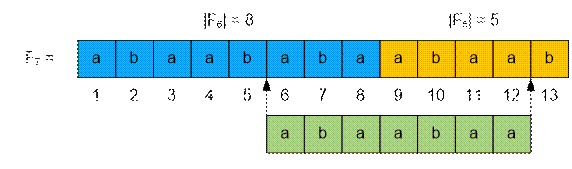
solve(7,
6, 12) = solve(7
– 1, 6, fib(6)) + solve(7 – 2, 1, 12 – fib(6)) =
= solve(6,
6, 8) + solve(5, 1, 4) = “aba” + “abaa” = “abaabaa”.
Algorithm realization
Let’s add the Fibonacci numbers to the fib
array: fib[i] contains the length of si.
#define MAX 44
int fib[MAX] = {0, 1};
Implement the function solve.
string solve(int n, int Left, int Right)
{
if (n == 1) return "b";
if (n == 2) return "a";
if (Right
<= fib[n-1]) return solve(n-1,
Left, Right);
if (Left >
fib[n-1])
return solve(n-2, Left - fib[n-1], Right -
fib[n-1]);
return
solve(n-1, Left, fib[n-1]) + solve(n-2, 1, Right -
fib[n-1]);
}
The main part of the program. Find
the first MAX Fibonacci numbers.
for(int
i = 2; i < MAX; i++)
fib[i] = fib[i-1] + fib[i-2];
Read the input data. Find and print the
answer.
scanf("%d %d %d",&n,&m,&l);
string res =
solve(n,m,m+l-1);
puts(res.c_str());
Java realization
import java.util.*;
public class Main
{
public static int MAX =
44;
public static int fib[] = new int[44];
public static
String solve(int n, int Left, int Right)
{
if (n ==
1) return "b";
if (n ==
2) return "a";
if (Right
<= fib[n-1])
return solve(n-1, Left, Right);
if (Left >
fib[n-1])
return solve(n-2, Left - fib[n-1], Right - fib[n-1]);
return solve(n-1, Left, fib[n-1])
+
solve(n-2,
1, Right - fib[n-1]);
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
fib[1] =
1;
for(int i = 2;
i < MAX; i++)
fib[i] = fib[i-1] +
fib[i-2];
int n = con.nextInt();
int m = con.nextInt();
int l = con.nextInt();
String res = solve(n,m,m+l-1);
System.out.println(res);
con.close();
}
}